from scipy.stats import bernoulli
from numpy.random import seed
ACoin = bernoulli(0.5)
ACoin.rvs()0Ontological modeling — formalizing a hypothesis of the data-generating process
One view of knowledge is that the mind maintains working models of parts of the world. ‘Model’ in the sense that it captures some of the structure in the world, but not all (and what it captures need not be exactly what is in the world—just what is useful). ‘Working’ in the sense that it can be used to simulate this part of the world, imagining what will follow from different initial conditions. As an example take the Plinko machine: a box with uniformly spaced pegs, with bins at the bottom. Into this box we can drop marbles:

The plinko machine is a ‘working model’ for many physical processes in which many small perturbations accumulate—for instance a leaf falling from a tree. It is an approximation to these systems because we use a discrete grid (the pegs) and discrete bins. Yet it is useful as a model: for instance, we can ask where we expect a marble to end up depending on where we drop it in, by running the machine several times—simulating the outcome.
Imagine that someone has dropped a marble into the plinko machine; before looking at the outcome, you can probably report how much you believe that the ball has landed in each possible bin. Indeed, if you run the plinko machine many times, you will see a shape emerge in the bins. The number of balls in a bin gives you some idea of how much you should expect a new marble to end up there. This ‘shape of expected outcomes’ can be formalized as a probability distribution (described below). Indeed, there is an intimate connection between simulation, expectation or belief, and probability, which we explore in the rest of this section.
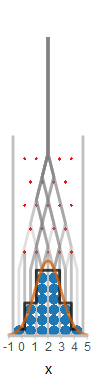
There is one more thing to note about our Plinko machine above: we are using a computer program to simulate the simulation. Computers can be seen as universal simulators. How can we, clearly and precisely, describe the simulation we want a computer to do?
We wish to describe in formal terms how to generate states of the world. That is, we wish to describe the causal process, or steps that unfold, leading to some potentially observable states. The key idea of this section is that these generative processes can be described as computations—computations that involve random choices to capture uncertainty about the process.
Programming languages are formal systems for describing what (deterministic) computation a computer should do. Modern programming languages offer a wide variety of different ways to describe computation; each makes some processes simple to describe and others more complex. However, a key tenet of computer science is that all of these languages have the same fundamental power: any computation that can be described with one programming language can be described by another. (More technically this Church-Turing thesis posits that many specific computational systems capture the set of all effectively computable procedures. These are called universal systems.)
Consider how we might simulate a coin being flipped, as random samples from a Bernoulli distribution.
from scipy.stats import bernoulli
from numpy.random import seed
ACoin = bernoulli(0.5)
ACoin.rvs()0If you run ACoin.rvs() multiple times you’ll see that you get 0 (\text{TAILS}) sometimes and 1 (\text{HEADS}) sometimes. Here we’ll run it 10 times in a row:
[ACoin.rvs() for _ in range(10)] ### make a list of ten sequential samples[0, 0, 1, 0, 1, 1, 0, 0, 1, 0]But what’s happening under the hood? It becomes clearer when we set a random seed:
def coin_flip():
"""This is the same as ACoin.rvs(random_state=100)"""
seed(100)
return ACoin.rvs()
[coin_flip() for _ in range(10)] ### a list of ten sequential samples[1, 1, 1, 1, 1, 1, 1, 1, 1, 1]Now when you evaluate coin_flip() multiple times, you’ll find that there is no more randomness. Our simulated coin always comes up \text{HEADS}.
Of course, this only happens because we set the random seed to the same value right before drawing each sample. If we were to sample ACoin multiple times without resetting the seed, we would draw different values, and in the limit of infinite samples, the proportion of \text{TAILS} and \text{HEADS} would be equal.
This trivial example illustrates a property of probability. A probability distribution is not a random process. When we write bernoulli(0.5) we’re assigning probability mass to subsets of the outcomes \{\text{TAILS}, \text{HEADS}\}. When we draw a sample by calling .rvs(), a (pseudo)random number is passed to a deterministic function that maps the state space of the random number generator to subsets of the outcomes.
In other words, one way of building generative models involves drawing samples according to specified distributions and collecting the results. For instance, let’s simulate 1000 flips of two fair coins and calculate how often they both come up \text{HEADS}:
seed(100)
FairCoin1 = bernoulli(0.5)
FairCoin2 = bernoulli(0.5)
n = 1000
both_heads = 0
for i in range(n):
if FairCoin1.rvs() == 1 and FairCoin2.rvs() == 1:
both_heads += 1
print(f"The coins both came up HEADS in {both_heads/n:0.3} proportion of the trials")The coins both came up HEADS in 0.234 proportion of the trialsBut it also often possible and preferable to calculate probabilities of interest directly. This is the approach taken by memo.
memo enables blazing fast generative modeling by compiling probabilistic models down to JAX array programs (Chandra et al., 2025).
Let’s explore how memo flips coins.
We’ll start by defining the sample space of a coin: S = \{ T, H \} (where T and H are \text{TAILS} and \text{HEADS}, which are represented by 0 and 1, respectively).
import jax
import jax.numpy as jnp
Coin1 = jnp.array(
[
0, # TAILS,
1, # HEADS
]
)JAX is a pretty amazing feat of engineering that sets a gold standard for performance. While widely used, it is still under active development, and at present, the focus on speed has involved compromises on safety and flexibility. For instance, notice that we can index the JAX array we defined similar to a numpy array:
Coin1[0]
Coin1[1]Array(0, dtype=int32)Array(1, dtype=int32)But unlike numpy, JAX does not prevent us from doing things that we should not be able to do, like indexing outside of the array:
Coin1[2]
Coin1[100]Array(1, dtype=int32)Array(1, dtype=int32)So when using JAX, it’s especially important to examine, probe and verify your code thoroughly. Incorrect indexing into multidimensional arrays is a common type of mistake, and JAX has few builtin protections. For more information, you can read about JAX’s sharp bits.
Information about some of the Common “Gotchas” in JAX
Now let’s write a memo model that enumerates over the sample space of the coin.
from memo import memo
Coin1 = jnp.array([0, 1])
@memo
def f[_c: Coin1]():
return _c
f()Array([0, 1], dtype=int32)The @memo model f returns the outcome _c in Coin1, so calling f() returns an array of every realization that _c can take. We can get a nice tabular printout using the print_table keyword when we call the model.
f(print_table=True)+-----------+----+
| _c: Coin1 | f |
+-----------+----+
| 0 | 0 |
| 1 | 1 |
+-----------+----+Array([0, 1], dtype=int32)JAX arrays are necessarily numeric, but it would be nice if we could define that \text{TAILS} ::= 0 and \text{HEADS} ::= 1 for the model. We can do that using IntEnum from the standard package enum.
from enum import IntEnum
class Coin(IntEnum):
TAILS = 0
HEADS = 1
@memo
def f_enum[_c: Coin]():
return _c
res = f_enum(print_table=True)+----------+---------+
| _c: Coin | f_enum |
+----------+---------+
| TAILS | 0 |
| HEADS | 1 |
+----------+---------+Let’s now have memo flip the coin. We do this using given2 by specifying the probability mass on each outcome.
The agent: given(x in X, wpp=f(x)) statement enumerates over the sample space (X) and assigns a weight (f(x)) to every possible value (x). Thus, the agent: given(x ...) statement constructs a random variable, agent.x, which is distributed according to P(X{=}x) = \frac{f(x)}{\sum_{x \in \mathcal{X}} f(x)} over sample space \mathcal{X}. The support of this distribution is the subset of \mathcal{X} where f(x) > 0. We can think of wpp as an acronym for “weight proportional to probability” or “with probability proportional to”. Since wpp implicitly normalizes the weights over the sample space, setting it to a constant pushes forward a uniform distribution. E.g. agent: given(x in X, wpp=len(X)), agent: given(x in X, wpp=1), and agent: given(x in X, wpp=5) all push forward P(X{=}x) = \frac{1}{|\mathcal{X}|}.
A key design principle of memo is encapsulation, meaning that information is bound to “frames” and is not automatically accessible from outside the frame. We’ll see how important this architecture is when we start modeling minds’ mental models of other minds’ mental models. For now, we’ll define an observer frame that represents the outcome c of the Coin flip. This information is bound to the observer’s mind, so we always need to access it within the observer frame (e.g. with observer.c).
Finally, we enumerate over {\_}{c} \in Coin and return the probability (Pr[...]) that the observer thinks that the outcome of the coin toss (observer.c) was _c.
@memo
def g[_c: Coin]():
observer: given(c in Coin, wpp=1)
return Pr[observer.c == _c]
res = g(print_table=True)+----------+------+
| _c: Coin | g |
+----------+------+
| TAILS | 0.5 |
| HEADS | 0.5 |
+----------+------+Query variables are specified in the function definition with square brackets (e.g. _c in def g[_c: Coin]():) and are bound to the outer-most frame (the @memo frame).
All other variables must be defined within internal frames. For instance, in the above example, c is bound to the observer frame via observer: given(c in Coin, ...).
I find it useful to clearly differentiate query variables from variables bound to internal frames.
In this course, I will typically use a convention of denoting query variables (i.e. all variables in the outer-frame) with a leading underscore (_c).
This is not strictly necessary, memo keeps these separate internally, such that one could also write
@memo
def g[c: Coin]():
observer: given(c in Coin, wpp=1)
return Pr[observer.c == c]in which case the c in observer: given(c in Coin, ...) refers to the c bound to observer whereas the c in Pr[... == c] refers to the c bound to the frame of the @memo function g.
Of course, not all distributions are uniform. We use wpp to specify the probability mass of outcomes.
E.g., to model a biased coin, we can specify that there’s greater probability mass on \text{TAILS} than on \text{HEADS}.
One way to do this is with a ternary.3 Rather than wpp=1, we can write
@memo
def f_ternary[_c: Coin]():
observer: given(c in Coin, wpp=0.8 if c == 0 else 0.2)
return Pr[observer.c == _c]
res = f_ternary(print_table=True)+----------+----------------------+
| _c: Coin | f_ternary |
+----------+----------------------+
| TAILS | 0.800000011920929 |
| HEADS | 0.20000000298023224 |
+----------+----------------------+Alternatively, we can define a custom probability mass function as a @jax.jit that we pass as wpp.
@jax.jit
def biased_coin_pmf(c):
return jnp.array([0.8, 0.2])[c]
@memo
def f_jit[_c: Coin]():
observer: given(c in Coin, wpp=biased_coin_pmf(c))
return Pr[observer.c == _c]
res = f_jit(print_table=True)+----------+----------------------+
| _c: Coin | f_jit |
+----------+----------------------+
| TAILS | 0.800000011920929 |
| HEADS | 0.20000000298023224 |
+----------+----------------------+Note that wpp normalizes the values passed to it (which is why wpp=1 forms a uniform distribution):
@jax.jit
def biased_coin_improper_pmf(c):
return jnp.array([16, 4])[c] ### NB the improper probability masses
@memo
def f_jit_autonorm[_c: Coin]():
observer: given(c in Coin, wpp=biased_coin_improper_pmf(c))
return Pr[observer.c == _c]
res = f_jit_autonorm(print_table=True)+----------+----------------------+
| _c: Coin | f_jit_autonorm |
+----------+----------------------+
| TAILS | 0.800000011920929 |
| HEADS | 0.20000000298023224 |
+----------+----------------------+Another sharp bit that memo inherits from JAX, is that there are no checks that the values you pass make sense.
It is up to you to insure that your probability functions are correct.
There are currently no protections against values that the violate the axioms of probability. E.g., it’s possible to propagate negative probabilities, and produce events with probabilities \gt 1 and \lt 0.
@memo
def f_improper[_c: Coin]():
1 observer: given(c in Coin, wpp=-0.8 if c == 0 else 0.2)
return Pr[observer.c == _c]
res = f_improper(return_pandas=True, return_xarray=True)
data = res.data
df = res.aux.pandas
xa = res.aux.xarray
### with the JAX array ###
# print(f"P(_c = T) = {data[0]:0.4f}")
# print(f"P(_c = H) = {data[1]:0.4f}")
### with the pandas df ###
# print(f"P(_c = T) = {df.loc[df['_c'] == 'TAILS', 'f_improper'].item():0.4f}")
# print(f"P(_c = H) = {df.loc[df['_c'] == 'HEADS', 'f_improper'].item():0.4f}")
### with xarray ###
print(f"P(_c = T) = {xa.loc['TAILS'].item():0.4f}")
print(f"P(_c = H) = {xa.loc['HEADS'].item():0.4f}")-0.8
P(_c = T) = 1.3333
P(_c = H) = -0.3333memo can package the results in a variety of ways. By default, a @memo returns a JAX array.
f_jit()Array([0.8, 0.2], dtype=float32)It is possible to additionally have @memo package the data in a 2D pandas DataFrame
df = f_jit(return_pandas=True).aux.pandas
print("DataFrame:")
print(df)
print("\nsliced:")
print(df.loc[df["_c"] == "HEADS"])DataFrame:
_c
0 TAILS 0.8
1 HEADS 0.2
sliced:
_c
1 HEADS 0.2And as an N-dimensional xarray with named axes and named indexes.
xa = f_jit(return_xarray=True).aux.xarray
xa<xarray.DataArray '' (_c: 2)> Size: 8B Array([0.8, 0.2], dtype=float32) Coordinates: * _c (_c) <U5 40B 'TAILS' 'HEADS'
xa.loc["HEADS"]<xarray.DataArray '' ()> Size: 4B
Array(0.2, dtype=float32)
Coordinates:
_c <U5 20B 'HEADS'These are not mutually exclusive.
res = f_jit(print_table=True, return_pandas=True, return_xarray=True)
### JAX array ###
res.data
### Pandas DataFrame ###
res.aux.pandas
### xarray ###
res.aux.xarray+----------+----------------------+
| _c: Coin | f_jit |
+----------+----------------------+
| TAILS | 0.800000011920929 |
| HEADS | 0.20000000298023224 |
+----------+----------------------+Array([0.8, 0.2], dtype=float32)| _c | ||
|---|---|---|
| 0 | TAILS | 0.8 |
| 1 | HEADS | 0.2 |
<xarray.DataArray '' (_c: 2)> Size: 8B Array([0.8, 0.2], dtype=float32) Coordinates: * _c (_c) <U5 40B 'TAILS' 'HEADS'
pandas and xarray are much slower than JAX, and conversion of types introduces additional overhead. It’s advisable to only convert your data as a terminal step.
In the process of building memo models, it’s often useful to examine a particular realization of a variable rather than enumerating over all possible values. For instance, we could have this @memo return the probability of \text{HEADS} alone by specifying Pr[observer.c == 1] rather than == _c.
from enum import IntEnum
class Coin(IntEnum):
TAILS = 0
HEADS = 1
@jax.jit
def biased_coin_pmf(c):
return jnp.array([0.8, 0.2])[c]
@memo
def f_query():
observer: given(c in Coin, wpp=biased_coin_pmf(c))
return Pr[observer.c == 1]
f_query(print_table=True)+----------------------+
| f_query |
+----------------------+
| 0.20000000298023224 |
+----------------------+Array(0.2, dtype=float32)You can also query the named element of an IntEnum class using curly brackets, e.g. {Coin.HEADS} rather than the value 1:
from enum import IntEnum
class Coin(IntEnum):
TAILS = 0
HEADS = 1
@memo
def f_query():
observer: given(c in Coin, wpp=biased_coin_pmf(c))
return Pr[observer.c == {Coin.HEADS}]
f_query(print_table=True)+----------------------+
| f_query |
+----------------------+
| 0.20000000298023224 |
+----------------------+Array(0.2, dtype=float32)Now that we’ve built a simple @memo, let’s extend it by tossing the coin multiple times.
Imagine that your teacher hands you a coin and says that you’ll get extra credit if it comes up \text{HEADS} at least once when you toss it two times.
@memo
def flip_twice_v1():
student: given(flip1 in Coin, wpp=1)
student: given(flip2 in Coin, wpp=1)
return Pr[student.flip1 + student.flip2 >= 1]
flip_twice_v1()Array(0.75, dtype=float32)But what if we want to flip the coin 10 or 1000 times? The approach of adding another given statement would be inefficient to scale. Fortunately, we can construct product spaces to handle this efficiently.
Here we make a product space4 of two flips of the coin.
from memo import domain as product
ProductSpaceTwoFlips = product(
f1=len(Coin),
f2=len(Coin),
)The result, ProductSpaceTwoFlips, is the Cartesian product of the sample space of the first flip and that of the second flip:
F_1 \times F_2 = \{ (T,T), (T,H), (H,T), (H,H) \}
for i in ProductSpaceTwoFlips:
print(ProductSpaceTwoFlips._tuple(i))(0, 0)
(0, 1)
(1, 0)
(1, 1)Evaluating ProductSpaceTwoFlips itself just returns the indices corresponding to these tuples.
ProductSpaceTwoFlips[0, 1, 2, 3]But you can access the underlying information in various ways:
ProductSpaceTwoFlips._tuple(2)
ProductSpaceTwoFlips.f1(2)
ProductSpaceTwoFlips.f2(2)(1, 0)10Again, mind the sharp bits.
ProductSpaceTwoFlips._tuple(100)(0, 0)We can now enumerate over all the events that can occur (where an event is the sequences of outcomes that results from flipping the coin twice): given(s in ProductSpaceTwoFlips, wpp=1) (remember that ProductSpaceTwoFlips evaluates to a list of integers, [0, 1, 2, 3]). To help keep the code tidy, we can define a @jax.jit function to sum the tuple.
@jax.jit
def sumflips(s):
return ProductSpaceTwoFlips.f1(s) + ProductSpaceTwoFlips.f2(s)
@memo
def flip_twice():
student: given(s in ProductSpaceTwoFlips, wpp=1)
return Pr[sumflips(student.s) >= 1]
flip_twice()Array(0.75, dtype=float32)Extending this to 10 flips is now straight forward. We simply define the sample space (now using dict comprehension to make {"f1": 2, ..., "f10": 2}) and dict unpacking (**dict()) to pass the contents to product() as keyword arguments. The result is len(SampleSpace) == 1024, which is the number of combinations that we expect (2^{10}).
We also see that each tuple, which represents a sequence of 10 flips, has the expected size (len(SampleSpace._tuple(0)) == 10).
Finally, we define a @jax.jit to sum this tuple. Here, we need to convert the tuple into a JAX array in order to sum it.
Of course, your teacher would just be giving extra credit away if you had 10 flips to get a single head, so she says that you need between 4 and 6 \text{HEADS} to win.
nflips = 10
SampleSpace = product(**{f"f{i}": len(Coin) for i in range(1, nflips + 1)})
@jax.jit
def sumseq(s):
return jnp.sum(jnp.array([SampleSpace._tuple(s)]))
@memo
def flip_n():
student: given(s in SampleSpace, wpp=1)
return Pr[sumseq(student.s) >= 4, sumseq(student.s) <= 6]
flip_n()Array(0.65625, dtype=float32)Looks like your teacher is still quite generous!
To test your understanding, make sure you can calculate this value.
For a range of outcomes, add the individual probabilities. We’ll use the binomial probability formula for each case:
\binom{n}{k} = \frac{n!}{k!(n - k)!}
For n=10 flips, the number of combinations is C(10, k) (10 choose k), and the probability of each combination is (1/2)^{10}, so the probability of k \text{HEADS}:
P({\#}{H} = k) = C(10,k) \cdot (1/2)^{10}
C(10, 4) = 210 combinations
P({\#}{H} = 4) = 210 \cdot (1/1024) = 210/1024
C(10, 5) = 252 combinations
P({\#}{H} = 5) = 252/1024
C(10, 6) = 210 combinations
P({\#}{H} = 6) = 210/1024
Thus, P(4 \leq {\#}{H} \leq 6) = (210 + 252 + 210)/1024 = 672/1024 \approx 0.65625
Imagine you have a deceptive teacher. After the second toss, she replaces the fair coin with a trick coin that only has a 10% chance of coming up \text{HEADS}.
We can calculate how much this will hurt your changes by specifying the probability mass on each flip, and then use those to get the probability mass on each sequence (which is what we need to pass as wpp).
Let’s start by visualizing the distribution of \text{HEADS} in a sequences of 10 flips of a fair coin.
from matplotlib import pyplot as plt
nflips = 10
SampleSpace = product(**{f"f{i}": len(Coin) for i in range(1, nflips + 1)})
### repackage into a JAX array, which we'll use for indexing
sample_space = jnp.array([SampleSpace._tuple(i) for i in SampleSpace])
fig, ax = plt.subplots()
# Create bins centered on integers: [-0.5, 0.5, 1.5, ..., 10.5]
bins = [i - 0.5 for i in range(nflips + 2)]
_ = ax.hist(sample_space.sum(axis=1).tolist(), bins=bins, color="blue", alpha=0.3)
_ = ax.axvline(4 - 0.5, color="red")
_ = ax.axvline(7 - 0.5, color="red")
_ = ax.set_xticks(range(nflips + 1))
_ = ax.set_ylabel("Number of sequences")
_ = ax.set_xlabel("Number of HEADS")
_ = ax.set_xlim((-0.5, nflips + 0.5))
(nheads, nsequences) = jnp.unique(sample_space.sum(axis=1), return_counts=True)
for (h, s) in zip(nheads.tolist(), nsequences.tolist()):
print(f"#HEADS: {h}, #sequences: {s}")#HEADS: 0, #sequences: 1
#HEADS: 1, #sequences: 10
#HEADS: 2, #sequences: 45
#HEADS: 3, #sequences: 120
#HEADS: 4, #sequences: 210
#HEADS: 5, #sequences: 252
#HEADS: 6, #sequences: 210
#HEADS: 7, #sequences: 120
#HEADS: 8, #sequences: 45
#HEADS: 9, #sequences: 10
#HEADS: 10, #sequences: 1
We’ll assign the probability mass for each flip in order to calculate the probably of each sequence.
### assign the probability mass for each flip
flip_probs_biased = (
jnp.full_like(
sample_space, jnp.nan, dtype=float
) ### init a new array with nans (for safety)
.at[jnp.where(sample_space == 1)] ### for every HEADS
.set(0.1) ### assign it prob 0.1
.at[jnp.where(sample_space == 0)] ### for every TAILS
.set(0.9) ### assign it prob 0.9
.at[:, :2] ### for the first two tosses
.set(0.5) ### use a fair coin
)
### make sure we didn't mess us out indexing in an obvious way
assert not jnp.any(jnp.isnan(flip_probs_biased))
### the probability of a sequence is the product of the individual flips
sequence_probs_biased = flip_probs_biased.prod(axis=1)
### make sure the probability mass function lies on the simplex
assert jnp.isclose(sequence_probs_biased.sum(), 1.0)
flip_probs_biasedArray([[0.5, 0.5, 0.9, ..., 0.9, 0.9, 0.9],
[0.5, 0.5, 0.9, ..., 0.9, 0.9, 0.1],
[0.5, 0.5, 0.9, ..., 0.9, 0.1, 0.9],
...,
[0.5, 0.5, 0.1, ..., 0.1, 0.9, 0.1],
[0.5, 0.5, 0.1, ..., 0.1, 0.1, 0.9],
[0.5, 0.5, 0.1, ..., 0.1, 0.1, 0.1]], dtype=float32)And compare the distributions
### assign the probability masses for the fair coin
flip_probs_unbiased = jnp.full_like(sample_space, 0.5, dtype=float)
sequence_probs_unbiased = flip_probs_unbiased.prod(axis=1)
assert jnp.isclose(sequence_probs_unbiased.sum(), 1.0)
def calc_probs(sequence_probs):
probs = []
for nheads in range(nflips + 1):
index = jnp.where(sample_space.sum(axis=1) == nheads)
probs.append(sequence_probs[index].sum().item())
return probs
fig, ax = plt.subplots()
ax.bar(
range(nflips + 1),
calc_probs(sequence_probs_unbiased),
facecolor="none",
edgecolor="black",
linewidth=3.0,
alpha=0.2,
label="Unbiased Game",
)
ax.bar(
range(nflips + 1),
calc_probs(sequence_probs_biased),
facecolor="blue",
alpha=0.2,
label="Deceptive Teacher",
)
ax.axvline(3.5, color="red")
ax.axvline(6.5, color="red")
_ = ax.set_ylabel("$probability$")
_ = ax.set_xlabel("Number of HEADS")
_ = ax.set_xticks(range(nflips + 1))
ax.legend()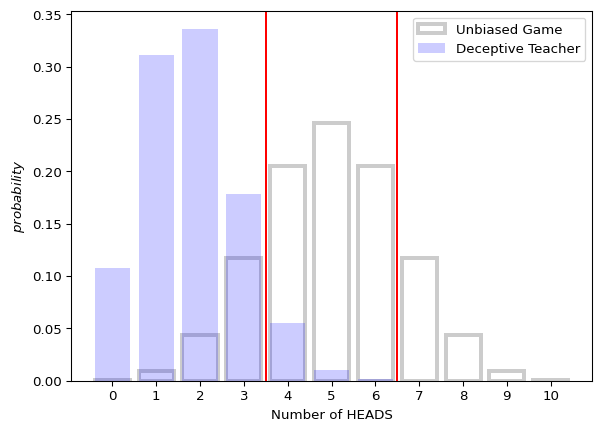
And now we can pass the probability mass we defined to wpp.
@jax.jit
def probfn_biased(s):
return sequence_probs_biased[s]
@jax.jit
def sumseq(s):
return jnp.sum(jnp.array([*SampleSpace._tuple(s)]))
@memo
def flip_game():
student: given(s in SampleSpace, wpp=probfn_biased(s))
return Pr[sumseq(student.s) >= 4, sumseq(student.s) <= 6]
flip_game()Array(0.06690599, dtype=float32)How much did your teacher’s trickery affect your chances?
A game of dice. You have 3 dice. The first die has 4 sides, the second has 6 sides, and third has 8 sides. You roll your three dice twice. The d4 is fair. The d6 is loaded such that there’s a 50% chance that it lands on 6, and a 10% chance that it lands on each other number. The d8 is fair for the first roll, then it’s dropped and chips in such a way that it’s 3x more likely to land on an even number than an odd number (all evens are equally likely, and all odds are equally likely).
Write a @memo that returns a JAX array with the probabilities of every possible combination of the dice in this game (i.e. across all rolls).
Write a @memo that returns the probability that the sum of the three dice on roll 2 is greater than or equal to the sum of the three dice on roll 1.
If you’re having trouble getting started, try making yourself a simpler version of the problem. E.g. start with (i) one unbiased 6-sided die rolled once, then (ii) two 6-six sided dice rolled once, (iii) two 6-sided dice rolled twice, (iv) two biased 6-sided dice rolled twice, etc.
You might find that it’s easier to build the model up in this fashion.
This is generally a good strategy for model building — start with the simplest thing and extended it one tiny piece at a time, checking that each piece is working the way you expect it to as you go.
%reset -f
import jax
import jax.numpy as jnp
from memo import memo, domain as product
D4 = jnp.arange(1, 4 + 1)
D6 = jnp.arange(1, 6 + 1)
D8 = jnp.arange(1, 8 + 1)
RollSampleSpace = product(
d4=len(D4),
d6=len(D6),
d8=len(D8),
)
SampleSpace = product(
r1=len(RollSampleSpace),
r2=len(RollSampleSpace),
)
@jax.jit
def pmf(s):
r1 = SampleSpace.r1(s)
r2 = SampleSpace.r2(s)
d4_r1 = RollSampleSpace.d4(r1)
d4_r2 = RollSampleSpace.d4(r2)
d6_r1 = RollSampleSpace.d6(r1)
d6_r2 = RollSampleSpace.d6(r2)
d8_r1 = RollSampleSpace.d8(r1)
d8_r2 = RollSampleSpace.d8(r2)
prob_d4_r1 = 1 / D4.size ### always fair
prob_d4_r2 = prob_d4_r1 ### same prob every roll
prob_d6_r1 = jnp.array([0.1, 0.1, 0.1, 0.1, 0.1, 0.5])[d6_r1] ### 0.5 if RollSampleSpace.d6(r1) == 6 - 1 else 0.1
prob_d6_r2 = jnp.array([0.1, 0.1, 0.1, 0.1, 0.1, 0.5])[d6_r2] ### 0.5 if RollSampleSpace.d6(r2) == 6 - 1 else 0.1
prob_d8_r1 = 1 / D8.size ### fair on roll 1
prob_d8_r2 = jnp.array([1/16, 3/16, 1/16, 3/16, 1/16, 3/16, 1/16, 3/16])[d8_r2] ### 3/16 if (RollSampleSpace.d8(r2) + 1) % 2 == 0 else 1/16
return prob_d4_r1 * prob_d4_r2 * prob_d6_r1 * prob_d6_r2 * prob_d8_r1 * prob_d8_r2
### assert that it's a proper pmf
assert jnp.isclose(jnp.sum(jnp.array([pmf(s) for s in SampleSpace])), 1.0)
@memo
def roll_dice[_s: SampleSpace]():
observer: given(s in SampleSpace, wpp=pmf(s))
return Pr[observer.s == _s]
res = roll_dice()
# print(res)
print("\n------\n")
### check that the probs sum to 1
print(res.sum())
### check that size of the output is what we expect
print(res.shape)
------
0.9999999
(36864,)%reset -f
import jax
import jax.numpy as jnp
from memo import memo, domain as product
D4 = jnp.arange(1, 4 + 1)
D6 = jnp.arange(1, 6 + 1)
D8 = jnp.arange(1, 8 + 1)
@memo
def roll_dice[_d4r1: D4, _d6r1: D6, _d8r1: D8, _d4r2: D4, _d6r2: D6, _d8r2: D8]():
observer: given(d4r1 in D4, wpp=1)
observer: given(d6r1 in D6, wpp=0.5 if d6r1 == 6 else 0.1)
observer: given(d8r1 in D8, wpp=1)
observer: given(d4r2 in D4, wpp=1)
observer: given(d6r2 in D6, wpp=0.5 if d6r2 == 6 else 0.1)
observer: given(d8r2 in D8, wpp=3 if d8r2 % 2 == 0 else 1)
return Pr[
observer.d4r1 == _d4r1,
observer.d6r1 == _d6r1,
observer.d8r1 == _d8r1,
observer.d4r2 == _d4r2,
observer.d6r2 == _d6r2,
observer.d8r2 == _d8r2,
]
res = roll_dice()
# print(res)
print("\n------\n")
### check that the probs sum to 1
print(res.sum())
### check that size of the output is what we expect
print(res.shape)
------
1.0002711
(4, 6, 8, 4, 6, 8)%reset -f
import jax
import jax.numpy as jnp
from memo import memo, domain as product
D4 = jnp.arange(1, 4 + 1)
D6 = jnp.arange(1, 6 + 1)
D8 = jnp.arange(1, 8 + 1)
RollSampleSpace = product(
d4=len(D4),
d6=len(D6),
d8=len(D8),
)
@jax.jit
def pmf_roll1(r1):
d4_r1 = RollSampleSpace.d4(r1)
d6_r1 = RollSampleSpace.d6(r1)
d8_r1 = RollSampleSpace.d8(r1)
prob_d4_r1 = 1 / D4.size ### always fair
prob_d6_r1 = jnp.array([0.1, 0.1, 0.1, 0.1, 0.1, 0.5])[d6_r1] ### 0.5 if RollSampleSpace.d6(r1) == 6 - 1 else 0.1
prob_d8_r1 = 1 / D8.size ### fair on roll 1
return prob_d4_r1 * prob_d6_r1 * prob_d8_r1
@jax.jit
def pmf_roll2(r2):
d4_r2 = RollSampleSpace.d4(r2)
d6_r2 = RollSampleSpace.d6(r2)
d8_r2 = RollSampleSpace.d8(r2)
prob_d4_r2 = 1 / D4.size ### always fair
prob_d6_r2 = jnp.array([0.1, 0.1, 0.1, 0.1, 0.1, 0.5])[d6_r2] ### 0.5 if RollSampleSpace.d6(r2) == 6 - 1 else 0.1
prob_d8_r2 = jnp.array([1/16, 3/16, 1/16, 3/16, 1/16, 3/16, 1/16, 3/16])[d8_r2] ### 3/16 if (RollSampleSpace.d8(r2) + 1) % 2 == 0 else 1/16
return prob_d4_r2 * prob_d6_r2 * prob_d8_r2
### assert that they are proper pmfs
assert jnp.isclose(jnp.sum(jnp.array([pmf_roll1(s) for s in RollSampleSpace])), 1.0)
assert jnp.isclose(jnp.sum(jnp.array([pmf_roll2(s) for s in RollSampleSpace])), 1.0)
@jax.jit
def sum_die(r):
return D4[RollSampleSpace.d4(r)] + D6[RollSampleSpace.d6(r)] + D8[RollSampleSpace.d8(r)]
@memo
def compare_rolls():
observer: given(r1 in RollSampleSpace, wpp=pmf_roll1(r1))
observer: given(r2 in RollSampleSpace, wpp=pmf_roll2(r2))
return Pr[sum_die(observer.r1) <= sum_die(observer.r2)]
compare_rolls()Array(0.56580013, dtype=float32)%reset -f
import sys
import platform
import importlib.metadata
print("Python:", sys.version)
print("Platform:", platform.system(), platform.release())
print("Processor:", platform.processor())
print("Machine:", platform.machine())
print("\nPackages:")
for name, version in sorted(
((dist.metadata["Name"], dist.version) for dist in importlib.metadata.distributions()),
key=lambda x: x[0].lower() # Sort case-insensitively
):
print(f"{name}=={version}")Python: 3.14.3 (main, Feb 4 2026, 01:51:49) [Clang 21.1.4 ]
Platform: Darwin 24.6.0
Processor: arm
Machine: arm64
Packages:
altair==6.0.0
annotated-types==0.7.0
anyio==4.12.1
anywidget==0.9.21
appnope==0.1.4
argon2-cffi==25.1.0
argon2-cffi-bindings==25.1.0
arrow==1.4.0
astroid==4.0.4
asttokens==3.0.1
async-lru==2.1.0
attrs==25.4.0
babel==2.18.0
beautifulsoup4==4.14.3
bleach==6.3.0
certifi==2026.1.4
cffi==2.0.0
cfgv==3.5.0
charset-normalizer==3.4.4
click==8.3.1
colour-science==0.4.7
comm==0.2.3
contourpy==1.3.3
cycler==0.12.1
debugpy==1.8.20
decorator==5.2.1
defusedxml==0.7.1
dill==0.4.1
distlib==0.4.0
distro==1.9.0
docutils==0.22.4
executing==2.2.1
fastjsonschema==2.21.2
filelock==3.20.3
fonttools==4.61.1
fqdn==1.5.1
h11==0.16.0
httpcore==1.0.9
httpx==0.28.1
identify==2.6.16
idna==3.11
importlib_metadata==8.7.1
ipykernel==7.2.0
ipython==9.10.0
ipython_pygments_lexers==1.1.1
ipywidgets==8.1.8
isoduration==20.11.0
isort==7.0.0
itsdangerous==2.2.0
jax==0.9.0.1
jaxlib==0.9.0.1
jedi==0.19.2
Jinja2==3.1.6
jiter==0.13.0
joblib==1.5.3
json5==0.13.0
jsonpointer==3.0.0
jsonschema==4.26.0
jsonschema-specifications==2025.9.1
jupyter-cache==1.0.1
jupyter-events==0.12.0
jupyter-lsp==2.3.0
jupyter_client==8.8.0
jupyter_core==5.9.1
jupyter_server==2.17.0
jupyter_server_terminals==0.5.4
jupyterlab==4.5.3
jupyterlab_pygments==0.3.0
jupyterlab_server==2.28.0
jupyterlab_widgets==3.0.16
kiwisolver==1.4.9
lark==1.3.1
marimo==0.19.9
Markdown==3.10.1
MarkupSafe==3.0.3
matplotlib==3.10.8
matplotlib-inline==0.2.1
mccabe==0.7.0
memo-lang==1.2.9
mistune==3.2.0
ml_dtypes==0.5.4
msgspec==0.20.0
narwhals==2.16.0
nbclient==0.10.4
nbconvert==7.17.0
nbformat==5.10.4
nest-asyncio==1.6.0
networkx==3.6.1
nodeenv==1.10.0
notebook_shim==0.2.4
numpy==2.4.2
numpy-typing-compat==20251206.2.4
openai==2.17.0
opt_einsum==3.4.0
optype==0.15.0
packaging==26.0
pandas==3.0.0
pandas-stubs==3.0.0.260204
pandocfilters==1.5.1
parso==0.8.5
pexpect==4.9.0
pillow==12.1.0
platformdirs==4.5.1
plotly==5.24.1
pre_commit==4.5.1
prometheus_client==0.24.1
prompt_toolkit==3.0.52
psutil==7.2.2
psygnal==0.15.1
ptyprocess==0.7.0
pure_eval==0.2.3
pycparser==3.0
pydantic==2.12.5
pydantic_core==2.41.5
Pygments==2.19.2
pygraphviz==1.14
pylint==4.0.4
pymdown-extensions==10.20.1
pyparsing==3.3.2
python-dateutil==2.9.0.post0
python-dotenv==1.2.1
python-json-logger==4.0.0
PyYAML==6.0.3
pyzmq==27.1.0
referencing==0.37.0
requests==2.32.5
rfc3339-validator==0.1.4
rfc3986-validator==0.1.1
rfc3987-syntax==1.1.0
rpds-py==0.30.0
ruff==0.15.0
scikit-learn==1.8.0
scipy==1.17.0
scipy-stubs==1.17.0.2
seaborn==0.13.2
Send2Trash==2.1.0
setuptools==81.0.0
six==1.17.0
sniffio==1.3.1
soupsieve==2.8.3
SQLAlchemy==2.0.46
stack-data==0.6.3
starlette==0.52.1
tabulate==0.9.0
tenacity==9.1.4
terminado==0.18.1
threadpoolctl==3.6.0
tinycss2==1.4.0
toml==0.10.2
tomlkit==0.14.0
tornado==6.5.4
tqdm==4.67.3
traitlets==5.14.3
typing-inspection==0.4.2
typing_extensions==4.15.0
tzdata==2025.3
uri-template==1.3.0
urllib3==2.6.3
uvicorn==0.40.0
virtualenv==20.36.1
wcwidth==0.6.0
webcolors==25.10.0
webencodings==0.5.1
websocket-client==1.9.0
websockets==16.0
widgetsnbextension==4.0.15
xarray==2026.1.0
zipp==3.23.0This section draws heavily from Goodman et al. (2016, Section Generative Models)↩︎
memo provides several random-variable-constructor verbs: draws, given, assigned, guesses, chooses. These are functionally identical (they alias to the same internal function), but their semantics allow us to make different epistemological expressions.↩︎
Ternary conditionals in Python take the form
value_if_true if condition else value_if_falseE.g.,
even = True if x % 2 == 0 else FalseTernary means “composed of three parts” (from the Latin ternarius).↩︎
For background on product spaces, see Michael Betancourt’s chapters,
↩︎