Intuitive theories 2 - What do we know?
The structure and content of mental models
Day 6: The structure and content of mental models
Last time we considered “Intuitive Theories”. Recall these passages from the papers we read:
What do we mean when we say that people’s knowledge is represented in the form of intuitive theories?
The basic idea is that people possess intuitive theories of different domains, such as physics, psychology, and biology, that are in some way analogous to scientific theories (Carey, 2009; Muentener & Bonawitz, this volume; Wellman & Gelman, 1992).
Like their scientific counterparts, intuitive theories are comprised of an ontology of concepts, and a system of (causal) laws that govern how the different concepts interrelate (Rehder, a, b, this volume).
The vocabulary of a theory constitutes a coherent structure that expresses how one part of the theory influences and is influenced by other parts of the theory.
A key characteristic of intuitive theories is that they do not simply describe what happened but interpret the evidence through the vocabulary of the theory.
A theory’s vocabulary is more abstract than the vocabulary that would be necessary to simply describe what happened.
Gerstenberg & Tenenbaum (2017)
The underlying cognitive representations can be understood as “intuitive theories,” with a causal structure resembling a scientific theory
…
we see model building as the hallmark of human-level learning, or explaining observed data through the construction of causal models of the world
…
Relative to physical ground truth, the intuitive physical state representation is approximate and probabilistic, and oversimplified and incomplete in many ways.
Lake et al. (2017)
An intuitive theory is a mental model of a domain (e.g. physics, psychology, etc.). A key phrase to remember is that “an intuitive theory is comprised of an ontology of concepts”. Let’s break this down what this means.
Concepts function as “atoms of thought”. For our immediate purposes, we can liken these to “symbols”.
Ontology implies categories and causal relationships.
An “ontology of concepts” implies that some domain is being mentally represented as causal relationships between abstract symbols.
And following the ideas that we established in previous sessions, we can additionally say that intuitive theories are probabilistic and generative.
By positioning intuitive theories as generative models, we can get deep into the weeds while simultaneously remembering that all we are doing is building more elaborate generative models. In order words, as we get into the minutia of causal modeling, remember that we can always step back and think of these models as \(P(\mathcal{H}{=}h) \, P(\mathcal{D} \mid \mathcal{H}{=}h)\), which is of course equal to \(P(\mathcal{H}{=}h, \, \mathcal{D})\), and use Bayes’ rule (which, again, is just a re-expression of conditional probability) to think about employing a generative model to predict, interpret, explain, and infer, things about the mind and world.
Last time we saw how probabilistic programs offer a natural formalism for modeling intuitive theories, with nodes functioning as symbols and directed edges functioning as causal relationships.
All of these ideas are going to be the main foundation that we build on. But before we get back to the topic of probabilistic programming, I want to spend a bit of time considering other aspects of intuitive theories.
For your consideration
Exercise (a)
Place a cup on the ground. Now hold a pingpong ball (or coin) between two fingers. Now, starting on the other side of the room, briskly walk towards the cup at a constant velocity. Your goal is to release the ball and have it land in the cup. Importantly, your velocity should not change (make sure you don’t slow down as you near the cup) and your only action should be opening your fingers (don’t propel the ball). It’s helpful to put the heel of you hand on your hip.
People tend to overshoot. This is crazy, right? We deal with gravity and velocity every day. It gets even weirder if you ask people to draw trajectories of balls rolling off table edges. People seem to systematically discount the horizontal velocity. Now, importantly, that’s true both for their embodied behavior (they actually drop the ball to late) and for their explicit reasoning (they discount the horizontal component when drawing the trajectory). But, people with some physics training tend to do better on both accounts, so it seems that people can correct their biases with explicit knowledge.
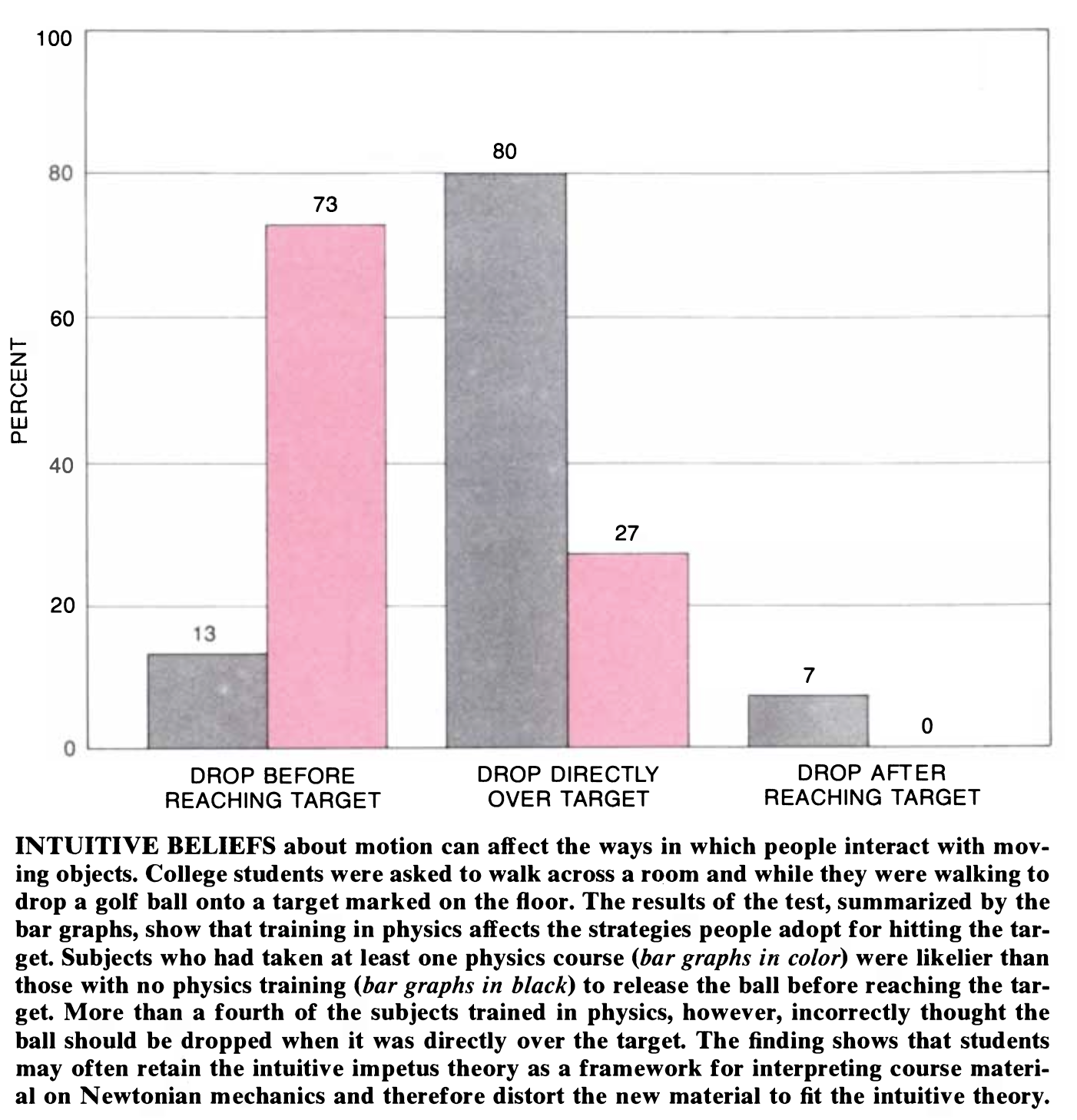McCloskey (1983)
Exercise (b)
Imagine swinging a ball on a string in a circle over your head, and then having the string’s attachment to the ball break. Draw this out and show where the ball goes. If you make a number of assumptions, the correct answer is that the ball will move in a straight line tangent to its previous orbit. However people often say that the ball will continue to curve as it moves. This is a really interesting case. While the tangent to the orbit is usually put forth by researcher as the “correct” answer (see below), the real world’s deviations from the requisite assumptions are often substantial.
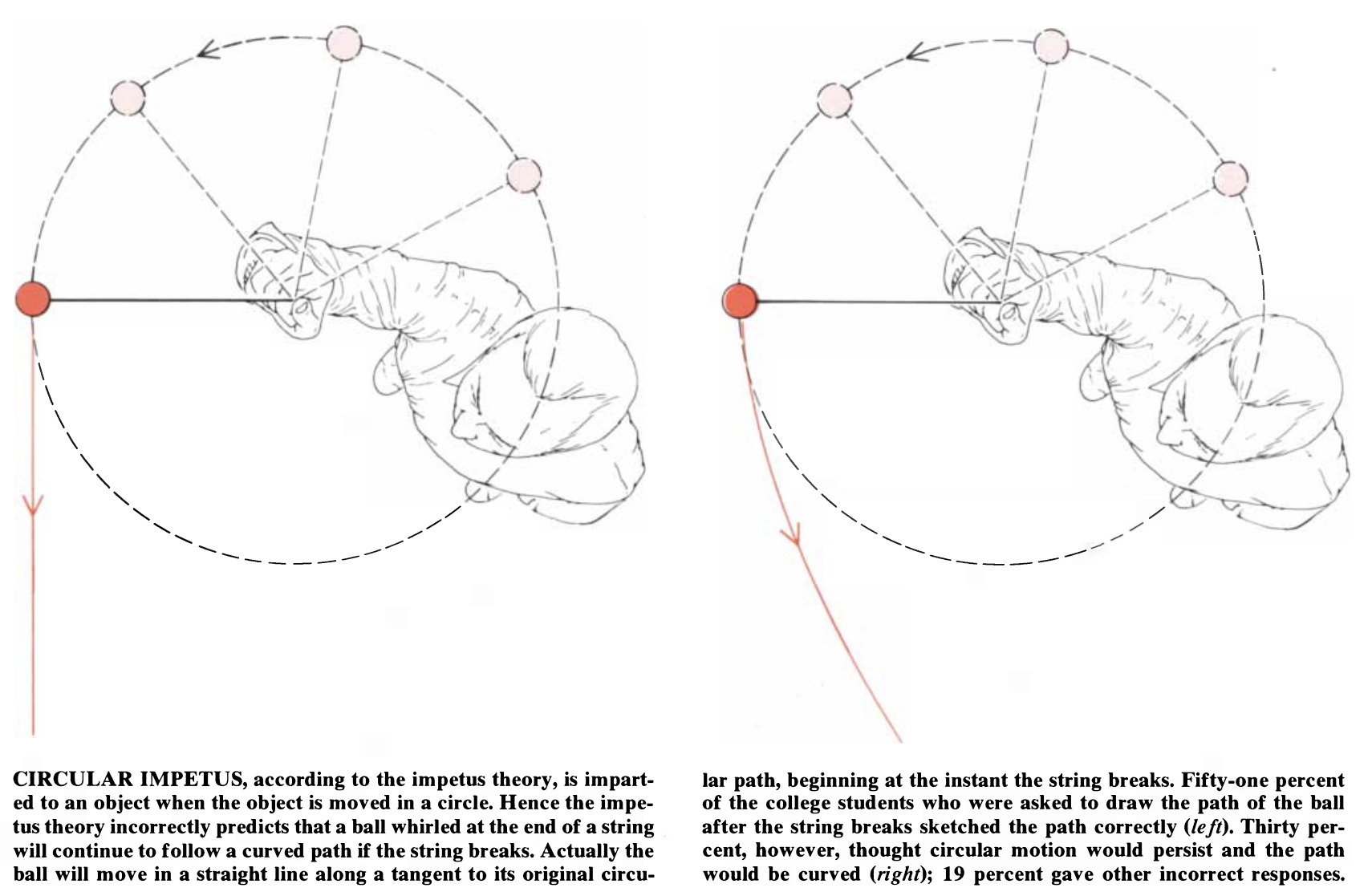McCloskey (1983)
Check out this video by All Things Physics (the whole video is great but if you’re in a hurry you can skip to the 11 minute mark): The Most Mind-Blowing Aspect of Circular Motion (All Things Physics)
In this case, people’s naïve intuitive theories seem to be reflecting some practical properties of the world (air drag, mass of the cord, propagation of the tension wave). And it’s not uncommon for physicists to over apply explicit theories of Newtonian physics under ideal assumption to real world phenomena.
Exercise (c)
Take 2 minutes and, from memory, draw the face of a one dollar bill in as much detail as you can. Bonus, take another 2 minutes to draw the back.
Now go compare your drawing to an actual bill. Yeah. Pretty shocking. Despite our many many encounters with one dollar bills, most people have very shallow explicit recall.
But people could probably detect some deviations. I.e. even when people can’t explicitly recall something, they might still have encoded something about it. Of course, people can also miss dramatic manipulations that they would find glaring once pointed out.
What’s going on here? One thing to consider from earlier discussions is how, when some statistical regularity is not behaviorally relevant, it might not be encoded by the organism. When that’s the case over a lifetime, that might result in large blindspots (e.g. insensitivities to certain phonemes). When that’s the case over over evolutionary timescales, the organism might not have the capacity to represent the information.
If it became relevant for you to memorize the details of a dollar bill, you almost certainly could. But let this example impress upon you that we shouldn’t assume that exposure, however extensive, is sufficient for someone to represent information.
Exercise (d)
Draw a bicycle, in as much detail as you can, in 2 minutes.
Most of us have a lot of behaviorally relevant interactions with bikes and bike parts. Even people who have ridden bicycles for hundreds of hours, changed tires, greased changes, etc. might draw bicycles that are comically unridable. This becomes all the more apparent when people’s drawing are rendered in 3d:
Artist Asks People to Draw a Bicycle from Memory and Renders the Results
Again, there’s a difference here between what people can explicitly produce in their drawing and what they could recognize as unrideable. Nevertheless, people tend to think they know (explicitly) what a bike looks like, and how it works to some degree, and are often shocked when they leave off critical components and configure other components in untenable ways. Why do we have this illusion of explanatory depth?
Drawings from class
Exercise (e)
Take 2 minutes to write instructions for someone who is learning how to ride a bike, how to turn right.
Now watch this short video by One Minute Physics: The Counterintuitive Physics of Turning a Bike (minutephysics)
Yeah. Basically no one learns that by riding bikes. (If you ride motorcycles, you probably learned it, what accounts for that difference?) While you might maintain that the previous examples are simply not relevant enough to behavior to have engendered accurate explicit knowledge, how to turn a bicycle is extremely behaviorally relevant once you’re on one. Anyone who has learned to ride knows how to do it. So we all know this implicitly (as in we do it automatically). And it’d probably be a great thing to explicitly tell people learning to ride. But most of us just pick it up via operant conditioning, and maintain a mistaken belief about what we’re physically doing indefinitely.
Requirements and non-requirements
Ok, so armed with these examples, let’s consider a few things about intuitive theories. We started off by saying what’s required of an intuitive theory (for our purposes: concepts/symbols/elements, a system of relationships between the elements that includes causal relationships, probabilistic representations, and generative structure). Let’s now consider what’s not required of an intuitive theory.
Intuitive theories need not be introspectable. In many domains, people demonstrate that they have much richer mental models than they can report on, and the things people explicitly report can be incongruent and contradictory what they seem to implicitly think/know/believe/represent. This course is keenly interested in the territory between what’s in people’s minds, and what people think is in their minds. Much of the art of cognitive science lies in illuminating this terrain. And this course’s emphasis on brining attention to your mental models, investigating the cognitive processes at the edge of your awareness, and reflecting on how your experience is constructed, is intended to give you tools for exploring that landscape.
Intuitive theories need not be accurate. We’ve previously talked about people’s various stances on whether mental representation need be isomorphic with the world. Accuracy is related but not identical (something can be accurate without being isomorphic and can be isomorphic without being accurate). The examples above, and many others that we will see in the coming weeks, make clear that people’s mental models are often highly inaccurate, even when it seems like there might be a good deal of pressure on optimizing for accuracy.
Intuitive theories need not be grounded in first person experience. In class I gave examples of congenitally blind people’s intuitive theories of sight, e.g. Kim et al. (2019, 2021). Some of the subsequent discussion revolved around the role of inductive constraints acquired from first person experience, and overhypotheses acquired via evolution.
Additional ideas
And finally, let’s consider some additional ideas.
What are the advantages of intuitive theories being “…approximate and probabilistic, and oversimplified and incomplete in many ways”? What about having a vocabulary “more abstract than the vocabulary that would be necessary to simply describe what happened”?
There are many ways of conceptualizing cognitive processes other than intuitive theories. For our immediate purposes, we’re primarily concerned with using the idea of intuitive theories to think about building formal models of the mind. But don’t mistake this for a commitment to intuitive theories, in the strongest sense, being the correct way of framing all cognition. Even the experiential examples above might be more consistent with other notions of cognition. Just to populate the space with some other ideas, let me point out a few from the community commentary of Lake et al. (2017).
…prior knowledge will offer the greatest leverage when it reflects the most pervasive or ubiquitous structures in the environment, including physical laws, the mental states of others, and more abstract regularities such as compositionally and causality. Together, these points comprise a powerful set of target goals for AI research. However, while we concur on these goals, we choose a differently calibrated strategy for accomplishing them. In particular, we favor an approach that prioritizes autonomy, empowering artificially agents to learn their own internal models and how to use them, mitigating their reliance on detailed configuration by a human engineer. (Matthew Botvinick, et al.)
Lake et al. argue persuasively that modelling human-like intelligence requires flexible, compositional representations in order to embody world knowledge. But human knowledge is too sparse and self-contradictory to be embedded in “intuitive theories.” We argue, instead, that knowledge is grounded in exemplar-based learning and generalization, combined with high flexible generalization, compatible both with non-parametric Bayesian modelling and with subsymbolic methods such as neural networks. (Nick Chater & Mike Oaksford)
Lake et al. propose that people rely on “start-up software,” “causal models,” and “intuitive theories” built using compositional representations to learn new tasks more efficiently than some deep neural network models. We highlight the many drawbacks of a commitment to compositional representations and describe our continuing effort to explore how the ability to build on prior knowledge and to learn new tasks efficiently could arise through learning in deep neural networks. (Steven S. Hansen, Andrew K. Lampinen, Gaurav Suri & James L. McClelland)
Lake et al. proposed a way to build machines that learn as fast as people do. This can be possible only if machines follow the human processes: the perception-action loop. People perceive and act to understand new objects or to promote specific behavior to their partners. In return, the object/person provides information that induces another reaction, and so on. (Ludovic Marin & Ghiles Mostafaoui)
References
Gerstenberg, T., & Tenenbaum, J. B. (2017). Intuitive Theories. In M. Waldmannn (Ed.), Oxford handbook of causal reasoning (pp. 515–548). Oxford University Press.
Kim, J. S., Aheimer, B., Montané Manrara, V., & Bedny, M. (2021). Shared understanding of color among sighted and blind adults. Proceedings of the National Academy of Sciences, 118(33), e2020192118. https://doi.org/10.1073/pnas.2020192118
Kim, J. S., Elli, G. V., & Bedny, M. (2019). Knowledge of animal appearance among sighted and blind adults. Proceedings of the National Academy of Sciences, 116(23), 11213–11222. https://doi.org/10.1073/pnas.1900952116
Lake, B. M., Ullman, T. D., Tenenbaum, J. B., & Gershman, S. J. (2017). Building machines that learn and think like people. Behavioral and Brain Sciences, 40, e253. https://doi.org/10.1017/S0140525X16001837
McCloskey, M. (1983). Intuitive Physics. Scientific American, 248(4), 122–131. http://www.jstor.org/stable/24968881
Next lecture notes: 7. Causal models 1 - how do we know?