test
test
For this to work, --exec has to be true
quarto render --profile production,notebook test-jupyter.qmd --execute --to ipynb --output-dir "/Users/dae/Downloads/comosoco-notebooks"The value is The radius of the circle is 10.
not notebook The radius of the circle is 10.
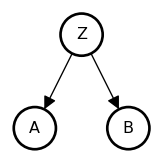
• A and B are associated: {A \not\perp B}
• Share a common cause Z
• Once stratified by Z, no association: {A \perp B \mid Z}
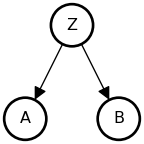
• A and B are associated: {A \not\perp B}
• Share a common cause Z
• Once stratified by Z, no association: {A \perp B \mid Z}
The Descendent
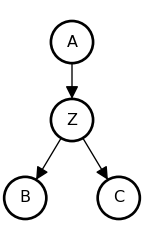
• A and B are causally associated through Z: {A \not\perp B}
• C holds information about Z
• Once stratified by C, A and B are less associated: {A \perp B \mid C} (if strong enough)
Conditional independence
Recall the definition of statistical (in)dependence. We define conditional (in)dependence in effectively the same way, just conditioning everything on a new random variable, Z. So whereas independence (i.e. ‘marginal’ independence) is defined as { A \perp B \iff P(A, \, B) = P(A) \; P(B) }, conditional independence is defined as
A \perp B \mid Z \iff P(A, \, B \mid Z) = P(A \mid Z) \; P(B \mid Z) \\ \forall~ (a, b, z) \in \{ A \times B \times Z \} ~~~\text{where}~~~ P(Z) > 0
And in the same way as we saw for marginal independence,
A \perp B \mid Z ~~\iff~~ P(A \mid B, \, Z) = P(A \mid Z)
The \iff symbol means “if and only if” (“iff”).
Exercise: Show that, if {A \perp B \mid Z}, then {P(B \mid A, \, Z) = P(B \mid Z)}. Hint: Follow the chain rule.
In general (regardless of dependence),
P(A, \, B \mid Z) = P(A \mid Z) \; P(B \mid A, \, Z) \\ \forall~ (a, b, z) \in \{ A \times B \times Z \} ~~~\text{where}~~~ P(A, \, Z) > 0
If {A \perp B \mid Z}, then {P(A, \, B \mid Z) = P(A \mid Z) \; P(B \mid Z)}.
In which case,
P(A \mid Z) \; P(B \mid Z) = P(A \mid Z) \; P(B \mid A, \, Z)
and {P(B \mid Z) = P(B \mid A, \, Z)}.