from enum import IntEnum
import jax.numpy as jnp
from memo import domain as product
from memo import memo
Die = jnp.arange(6) + 1
Dice = product(d1=Die.size, d2=Die.size)
class Coin(IntEnum):
TAILS = 0
HEADS = 1
class Outcome(IntEnum):
LOSE = 0
WIN = 1
def sum_dice(d):
return Die[Dice.d1(d)] + Die[Dice.d2(d)]Causal superseding
Modeling sufficiency and necessity in causal attribution
Inspired by: Kominsky et al. (2015), “Expt. 4”.
Domain
Memo Models
Conjunctive structure
Win iff (\text{coin}{=}H) \land (\text{dice} > \theta)
@no_type_check
@memo
def conjunctive_sufficiency[_coin: Coin](threshold, saliency):
"""
Sufficiency: P(Y_{C←c, D←D*} = win)
Potential outcome Y under intervention do(C=c) with counterfactual dice
D* ~ P(D) · exp(-λ · 𝟙[D > θ]), where λ is the saliency parameter.
"""
observer: thinks[
alex: draws(d in Dice, wpp=1),
alex: draws(c in Coin, wpp=1),
alex: assigned(result in Outcome,
wpp=1 if result == (sum_dice(d) > threshold and c == {Coin.HEADS}) else 0),
]
observer: observes_that[sum_dice(alex.d) == 12]
observer: observes_that[alex.c == {Coin.HEADS}]
return observer[wonders[
do(alex.c is _coin),
do(alex.d, wpp=exp(-saliency * (sum_dice(d) > threshold))),
E[alex.result == {Outcome.WIN}]
]]
@no_type_check
@memo
def conjunctive_necessity[_coin: Coin](threshold):
"""
Necessity: P(Y_{C←c, D←d} = win)
Potential outcome Y under intervention do(C=c), holding dice at
factual value d (here d s.t. sum(d) = 12).
"""
observer: thinks[
alex: draws(d in Dice, wpp=1),
alex: draws(c in Coin, wpp=1),
alex: assigned(result in Outcome,
wpp=1 if result == (sum_dice(d) > threshold and c == {Coin.HEADS}) else 0),
]
observer: observes_that[sum_dice(alex.d) == 12]
observer: observes_that[alex.c == {Coin.HEADS}]
return observer[wonders[
do(alex.c is _coin),
E[alex.result == {Outcome.WIN}]
]]Disjunctive structure
Win iff (\text{coin}{=}H) \lor (\text{dice} > \theta)
@no_type_check
@memo
def disjunctive_sufficiency[_coin: Coin](threshold, saliency):
"""
Sufficiency: P(Y_{C←c, D←D*} = win)
Potential outcome Y under intervention do(C=c) with counterfactual dice
D* ~ P(D) · exp(-λ · 𝟙[D > θ]).
"""
observer: thinks[
alex: draws(d in Dice, wpp=1),
alex: draws(c in Coin, wpp=1),
alex: assigned(result in Outcome,
wpp=1 if result == (sum_dice(d) > threshold or c == {Coin.HEADS}) else 0),
]
observer: observes_that[sum_dice(alex.d) == 12]
observer: observes_that[alex.c == {Coin.HEADS}]
return observer[wonders[
do(alex.c is _coin),
do(alex.d, wpp=exp(-saliency * (sum_dice(d) > threshold))),
E[alex.result == {Outcome.WIN}]
]]
@no_type_check
@memo
def disjunctive_necessity[_coin: Coin](threshold):
"""
Necessity: P(Y_{C←c, D←d} = win)
Potential outcome Y under intervention do(C=c), holding dice at
factual value d.
"""
observer: thinks[
alex: draws(d in Dice, wpp=1),
alex: draws(c in Coin, wpp=1),
alex: assigned(result in Outcome,
wpp=1 if result == (sum_dice(d) > threshold or c == {Coin.HEADS}) else 0),
]
observer: observes_that[sum_dice(alex.d) == 12]
observer: observes_that[alex.c == {Coin.HEADS}]
return observer[wonders[
do(alex.c is _coin),
E[alex.result == {Outcome.WIN}]
]]Computing measures
def get_measures(saliency=1.0):
"""Compute sufficiency and necessity for all conditions via memo."""
conditions = [
('conj_likely', conjunctive_sufficiency, conjunctive_necessity, 2),
('conj_unlikely', conjunctive_sufficiency, conjunctive_necessity, 11),
('disj_likely', disjunctive_sufficiency, disjunctive_necessity, 2),
('disj_unlikely', disjunctive_sufficiency, disjunctive_necessity, 11),
]
results = {}
for name, sufficiency_fn, necessity_fn, threshold in conditions:
sufficiency = float(sufficiency_fn(threshold, saliency)[Coin.HEADS])
necessity = 1 - float(necessity_fn(threshold)[Coin.TAILS])
results[name] = {'sufficiency': sufficiency, 'necessity': necessity}
return resultsResults
Sufficiency and necessity across four conditions (threshold \theta \in \{2, 11\}, structure \in \{\land, \lor\}):
import numpy as np
from matplotlib import pyplot as plt
from matplotlib.patches import Patch
# Pre-computed measures (saliency λ = 1.0)
measures = {
'conj_likely': {'sufficiency': 0.8824, 'necessity': 1.0},
'conj_unlikely': {'sufficiency': 0.0270, 'necessity': 1.0},
'disj_likely': {'sufficiency': 1.0, 'necessity': 0.0},
'disj_unlikely': {'sufficiency': 1.0, 'necessity': 0.0},
}
cond_order = ['conj_likely', 'conj_unlikely', 'disj_likely', 'disj_unlikely']
print(f"{'Condition':<18} {'Sufficiency':>12} {'Necessity':>10}")
print("-" * 45)
for c in cond_order:
m = measures[c]
print(f"{c:<18} {m['sufficiency']:>12.4f} {m['necessity']:>10.4f}")Condition Sufficiency Necessity
---------------------------------------------
conj_likely 0.8824 1.0000
conj_unlikely 0.0270 1.0000
disj_likely 1.0000 0.0000
disj_unlikely 1.0000 0.0000Empirical data
Causal ratings from Kominsky (2015), Experiment 4 (7-point scale):
empirical = {
'conj_likely': 5.19,
'conj_unlikely': 2.88,
'disj_likely': 4.27,
'disj_unlikely': 4.46,
}
empirical_scaled = {k: v / 7 for k, v in empirical.items()}Model fitting
Fit \beta via least squares: \text{rating} = \beta \cdot S + (1-\beta) \cdot N
def fit_beta(measures, empirical):
"""Fit β in: rating = β·sufficiency + (1-β)·necessity"""
conditions = list(measures.keys())
suff = np.array([measures[c]['sufficiency'] for c in conditions])
nec = np.array([measures[c]['necessity'] for c in conditions])
y = np.array([empirical[c] for c in conditions])
# rating = β·suff + (1-β)·nec = nec + β·(suff - nec)
diff = suff - nec
y_centered = y - nec
beta = np.dot(diff, y_centered) / np.dot(diff, diff)
return float(np.clip(beta, 0, 1))
beta = fit_beta(measures, empirical_scaled)
print(f"Fitted β = {beta:.4f}")Fitted β = 0.6250Predictions
def compute_r2(predicted, actual):
"""Compute R² between predicted and actual values."""
conditions = list(predicted.keys())
y_pred = np.array([predicted[c] for c in conditions])
y_true = np.array([actual[c] for c in conditions])
ss_res = np.sum((y_true - y_pred) ** 2)
ss_tot = np.sum((y_true - np.mean(y_true)) ** 2)
return 1 - ss_res / ss_tot
model_preds = {
c: beta * measures[c]['sufficiency'] + (1 - beta) * measures[c]['necessity']
for c in measures
}
r2 = compute_r2(model_preds, empirical_scaled)
print(f"R² = {r2:.4f}")R² = 0.3863Code
fig, axes = plt.subplots(1, 2, figsize=(10, 4))
positions = [0.75, 1.25, 1.75, 2.25]
bar_width = 0.4
light_grey, dark_grey = "#AAAAAA", "#444444"
colors = [light_grey, dark_grey, light_grey, dark_grey]
for ax, data, title in [
(axes[0], empirical_scaled, "Empirical"),
(axes[1], model_preds, f"Model (R² = {r2:.2f})")
]:
values = [data[c] for c in cond_order]
ax.bar(positions, values, width=bar_width, color=colors, edgecolor='black')
ax.set_ylim(0, 1.1)
ax.set_xlim(0.25, 2.75)
ax.set_xticks([1, 2])
ax.set_xticklabels(["Conjunctive", "Disjunctive"])
ax.set_ylabel("Rating (scaled)")
ax.set_title(title)
fig.legend([Patch(facecolor=light_grey, edgecolor='black'),
Patch(facecolor=dark_grey, edgecolor='black')],
['Likely (θ=2)', 'Unlikely (θ=11)'],
loc='upper right', bbox_to_anchor=(0.98, 0.88))
plt.tight_layout()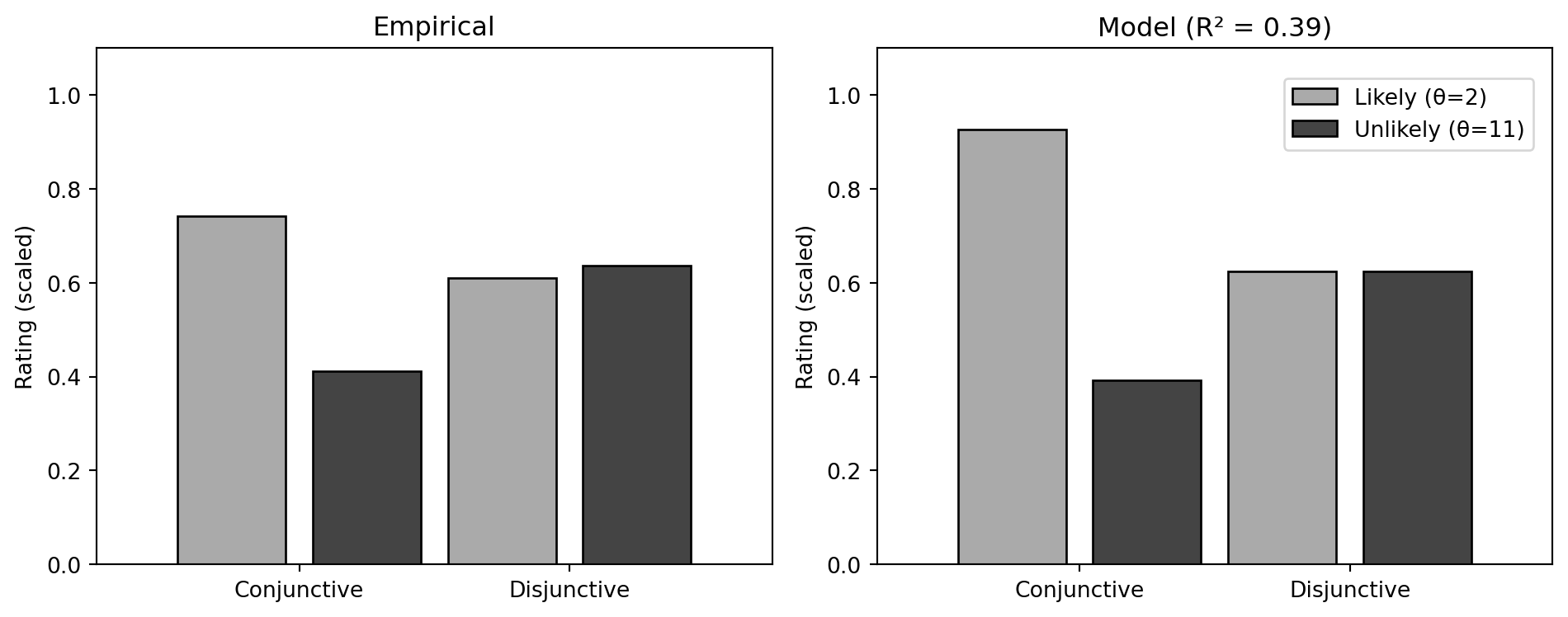
Model comparison
models = {
'Sufficiency only': {c: measures[c]['sufficiency'] for c in measures},
'Necessity only': {c: measures[c]['necessity'] for c in measures},
'β·S + (1-β)·N': model_preds,
}
print(f"{'Model':<20} {'R²':>10}")
print("-" * 35)
for name, preds in models.items():
r2 = compute_r2(preds, empirical_scaled)
print(f"{name:<20} {r2:>10.4f}")Model R²
-----------------------------------
Sufficiency only -6.9140
Necessity only -19.8855
β·S + (1-β)·N 0.3863print(f"\n{'Condition':<16} {'Emp':>8} {'Suff':>8} {'Nec':>8} {'Model':>8}")
print("-" * 55)
for c in cond_order:
print(f"{c:<16} {empirical_scaled[c]:>8.3f} "
f"{measures[c]['sufficiency']:>8.3f} "
f"{measures[c]['necessity']:>8.3f} "
f"{model_preds[c]:>8.3f}")
Condition Emp Suff Nec Model
-------------------------------------------------------
conj_likely 0.741 0.882 1.000 0.927
conj_unlikely 0.411 0.027 1.000 0.392
disj_likely 0.610 1.000 0.000 0.625
disj_unlikely 0.637 1.000 0.000 0.625References
Kominsky, Jonathan F., Phillips, Jonathan, Gerstenberg, Tobias, Lagnado, David, & Knobe, Joshua. (2015). Causal superseding. Cognition, 137, 196–209. https://doi.org/10.1016/j.cognition.2015.01.013